Magnetic potential

Many of our Magnetism A-Z pages contain formulas that can only be illustrated with Javascript. We recommend to enable Javascript if you want to view these pages.

What is the magnetic potential?

The magnetic potential describes the magnetic field between the north and south poles, taking into account the distance between the poles. If the magnetic field is very strong at a particular location, the magnetic potential is also correspondingly large. The same applies in the field of electronics. The electric potential is equal to the electric field multiplied by the distance between the poles. A large electric field with a large distance between the poles can only be generated with a correspondingly high voltage.

Table of Contents

Excursus: Electric potential

Just as electric fields are used to define an electric potential, magnetic fields can also be used to define a magnetic potential. To do this, it is helpful to recall the electric context:

If an electric potential (U) of, say, 1 000 volts is applied between two electrically charged capacitor plates and there is a distance (d) of 1 metre between these capacitor plates, the electric field (E) can be directly determined: the following applies:

\(E=\frac{U}{d}\)
The electric field is therefore 1 000 V/m.

Conversely, the electric potential between the plates can be obtained by multiplying the electric field (if this is constant along the path) by the length of the path, i.e. the distance between the plates.

If the electric field is dependent on the location (x), the electric potential must be calculated using a path integral over the electric field:

\(U=\int_{0}^d E(x)dx\)
where, as before, if E is location-independent, it can simply be multiplied by the path length d:

\(U=\int_{0}^d Edx=E\cdot{d}\)
You can imagine the electric potential as the force of a pump that pumps charges in an electrical circuit like water in a water circuit.

The amount of water corresponds to the current and, for a given pumping force (potential), depends only on the diameter of the pipes (resistance). The power (P) of the pump corresponds to the product of the pumping force (potential, U) and the amount of water (current, I) :

P=U•I

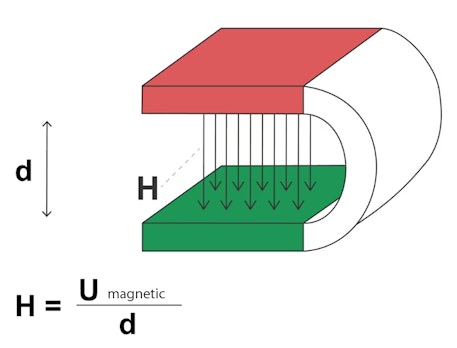
The illustration demonstrates the relationship between the magnetic potential U between the north pole and south pole of the horseshoe magnet and the magnetic field strength H. The formula only applies to the simple case of a location-independent magnetic field H. If a horseshoe magnet has a magnetic field of strength H and the poles are at distance d, the magnetic potential between the poles is U=H•d. If the distance is greater, the potential between the poles must be greater to achieve the same field.

Definition of magnetic potential

The magnetic potential can be thought of in the same way as the electric potential. The potential between two magnetic poles at a constant distance exerts a force on magnetic moments that is proportional to the magnetic potential. Therefore, if the poles are at a constant distance, the magnetic field is proportional to the magnetic potential.

The magnetic potential is thus related to the magnetic field in the same way that the electric potential is related to the electric field:

The magnetic field H must be multiplied by the distance d between the poles that generate this field to obtain the magnetic potential. If the magnetic field between the poles is constant (e.g., in a horseshoe magnet), the following applies:

U_{magnetisch}=\int_{0}^d Hdx=H\cdot{d}

The magnetic flux Φ is equivalent to the electric current. A magnetic resistance R_mag can therefore also be defined using the magnetic potential U_mag and the magnetic flux Φ:

\(R_{mag}=\frac{U_{mag}}{\Phi}\)
In materials with high magnetic permeability the magnetic flux is very high. The magnetic resistance is indirectly proportional to the magnetic flux and therefore indirectly proportional to the magnetic permeability. Although a superconductor has no electrical resistance, it has an infinitely large magnetic resistance. The magnetic permeability of a superconductor is zero.

Author:
Dr Franz-Josef Schmitt

Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.

The copyright for all content in this compendium (text, photos, illustrations, etc.) remains with the author, Franz-Josef Schmitt. The exclusive rights of use for this work remain with Webcraft GmbH, Switzerland (as the operator of supermagnete.ro). Without the explicit permission of Webcraft GmbH, the contents of this compendium may neither be copied nor used for any other purpose. Suggestions to improve or praise for the quality of the work should be sent via e-mail to [email protected]
© 2008-2025 Webcraft GmbH